당신이 무엇을 배우고 있다는것은 어제의 당신보다 훨씬 높은 가치가 되었다는 것이다

1. 위상 정렬 

: 스킬트리도 그 중 하나지.  

[1] 알고리즘 위상정렬 

: 순서를 정해보자 

ⓐ : 정의 

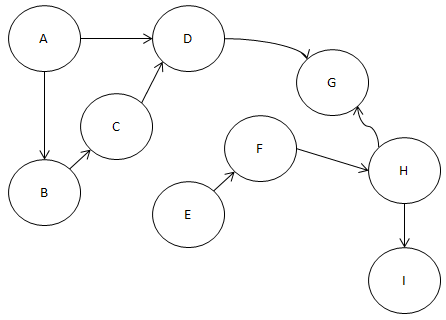
오늘은 위상 정렬에 대해서 하도록 하겠습니다. 

이게 대체 무엇을 하는 알고리즘일까요? 

음. 쉬운 예를 들어봅시다. 

Rpg 게임 한 번 쯤 해봤다면 

어떤 스킬을 배우는 데 필요한 조건이 있을 겁니다. 

즉, 어떤 스킬과 전제가 되는 스킬은 

서로 선후관계가 있는 것이죠? 

자. 메이플 같은 경우에도 

1차 Sp를 다 투자해야 2차 스킬을 배울 수 있어요. 

이런 선행 관계도 있지요? 

자. 이러한 관계를 

차근 차근 정리해 주는 알고리즘이 위상 정렬입니다. 

실생활에서도 이러한 예는 쉽게 찾아볼 수 있죠. 

예를 들어서 어떤 과목을 배우기 위한 선수 과목. 

이 둘의 관계 역시 선후 관계잖아요? 

자. 위상 정렬은 순서를 정해주는 알고리즘입니다. 

그러면 사이클이 있거나 

방향성이 없다면 

순서가 정해질 수 있을까요? 

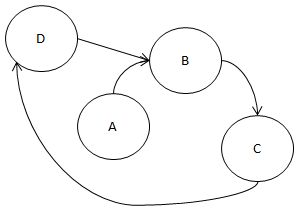
당연히 순서가 정해질 수 없을 겁니다. 

B를 먼저 하고 C를 그 다음에 하고 

그 다음에 D를 하고 다시 B를 하고.. 

이런 식으로 순서가 정해질 수 없죠. 

즉, 그래프가 DAG여야 위상 정렬이 가능합니다. 

이게 무슨 약자냐고요? 

Directed Acycilc Graph 

맞나 모르겠네. 방향이 있는 비순환 그래프. 

자. 일단  코드를 먼저 보고 

설명을 드리도록 하겠습니다. 

ⓑ : 코드 보기 

저 같은 경우 위상 정렬을 하기 위해

자료구조를 이렇게 정의했습니다.

Count는 들어오는 간선의 수고요.

Order는 순서 중 하나를 저장하기 위한 배열이고요.

사실 이것 외에는 별 것이 없어 보입니다.

일단 이 부분 뭔지는 모르겠는데

for문이 2번 돌아가는 걸로 봐서는

시간 복잡도가 O(MT) 정도 되겠네요.

그리고 이 부분을 봅시다.

진입 간선이 없는 노드를 선택하는 데

사실 이 알고리즘은 시간 복잡도가 O(N)

그 노드를 불러와서

진출 간선을 제거하는 데 O(N)

그리고 그것을 N번 수행하니까

사실 O(N^2)꼴로 정리가 되긴 합니다.

물론 N은 가수의 수니까

위상 정렬의 그래프로 따지면

노드의 수 정도 되겠지요.

일단 이 알고리즘에 대해서

먼저 설명해 드리도록 하죠.

코드가 길어 보여도

주석은 충분히 달아놨기 때문에

별로 어렵지 않을 겁니다. 

그래도 이해 안 가시는 분들을 위해서 

그림으로 자세히 설명해 드립니다. 

ⓒ : 예제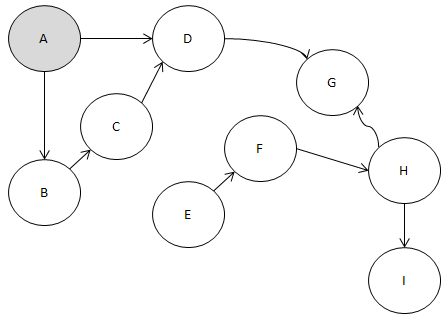

일단 우리는 다음과 같이 생각해 봅시다.

일단 진입 간선이 0개인 녀석을 찾습니다.

그리고 그 녀석을 찾으면

그 녀석에서 빠져 나가는 간선을 모두 제거합시다.

음. 예를 들어서

만약에 A라는 스킬을 찍어야 B를 찍을 수 있다는 관계가 있다면

일단 A라는 스킬을 가지고 있는 노드는

선행 조건이 없잖아요.

그리고 B라는 스킬은

A라는 스킬을 찍었다는 전제 하에서는

선행 조건이 또 없지요.

그런 이야기 입니다.

자. 일단 진입 간선의 수가 0인 노드 A를 봅시다.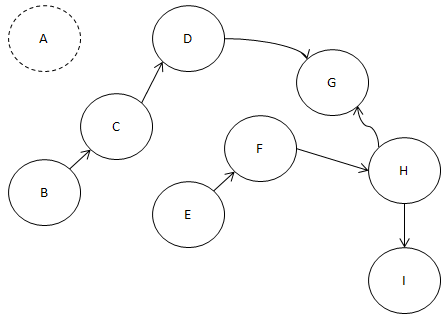

노드 A에서 나가는 진출 간선 2개를

제거하면 이렇게 되지요?

그리고 진입 간선이 0개인 노드를 찾읍시다.

B와 E가 남았죠?

알파벳 순으로 빠른 B를 뽑죠.

그러면 B에서 나가는 간선이 제거되겠군요.

다시. 이게 뭘 의미하느냐.

내가 B라는 스킬을 찍었다는 것을 의미해요.

일정한 레벨 이상으로.

B라는 스킬을 일정 레벨 이상 찍었을 때

C라는 스킬을 찍을 수 있다고 해 봐요.

만약 내가 B라는 스킬을 일정 레벨 이상 찍으면

C라는 스킬은 다른 조건 없이 찍을 수 있잖아요?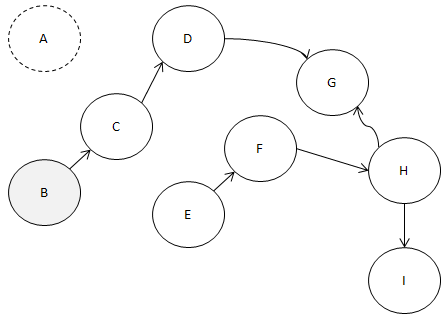

B를 선택해서 B에서 나가는 간선을

모두 제거하도록 합시다.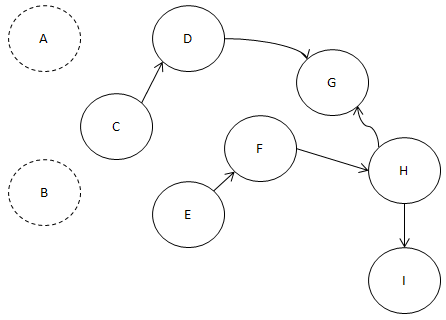

그러면 관계가 이렇게 나오는 군요.

이제 다시 한 번 볼까요?

C와 E가 아무런 조건 없이 수행될 수 있죠?

이 중 알파벳 순으로 빠른 노드를 찾으면 C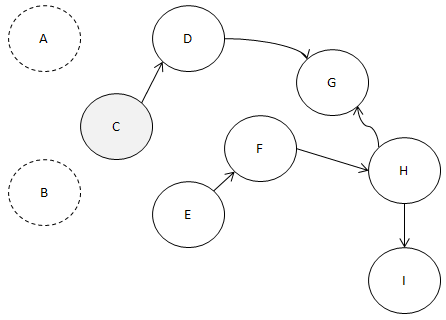

맞아요? 진입 간선 수가 0이니까요.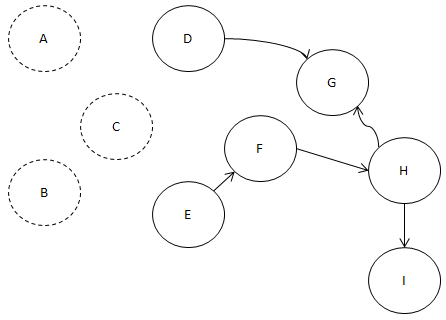

C에서 나가는 간선을 모두 제거하고

이제 남은 녀석들을 봅시다.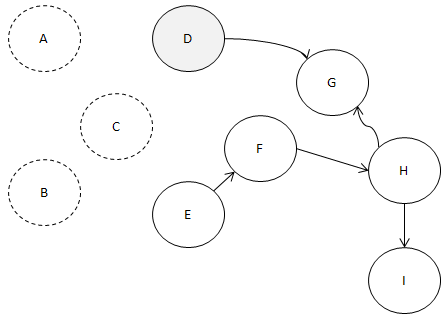

D와 E라는 녀석 말이죠.

진입 간선이 0개입니다.

맞죠? 이 중에서 알파벳 순으로 빠른

D를 먼저 빼 보지요.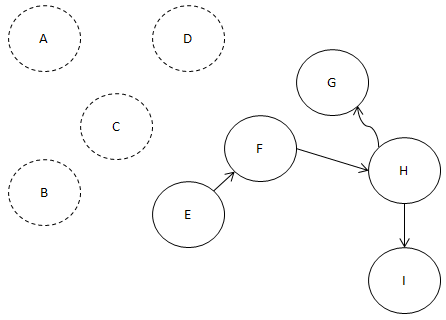

그러면 이렇게 되는군요.

D에서 나가는 간선도 제거했고요.

E로 진입하는 간선이 0개죠?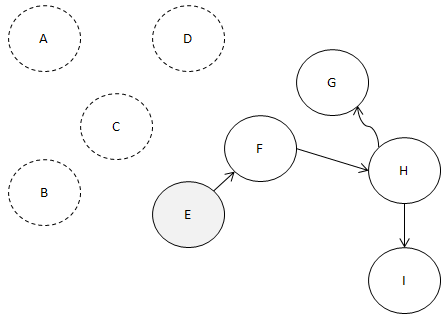

그렇죠? 맞지요?

따라서 E와 E에서 나가는 간선을 제거합니다.

그러면 이렇게 남는군요. 냠냠.

자. F로 들어오는 간선이 1개도 없습니다.

나머지는 1개씩 있는 상태죠..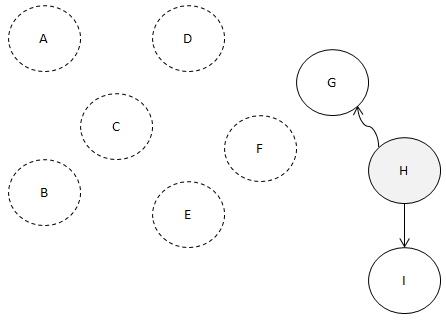

F를 출력해 주시고

이렇게 나왔네요.

F에서 나가는 간선도 제거했으니 말이죠.

H로 들어오는 간선이 없죠?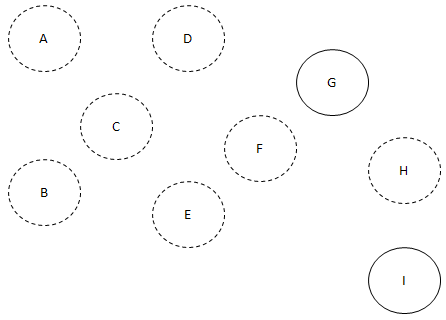

H와 H에서 나가는 간선을 제거해 줍시다.

그러면 G와 I 이렇게 2개가 남습니다.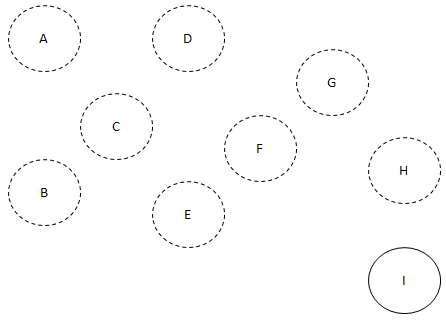

차례 차례 제거하도록 합시다.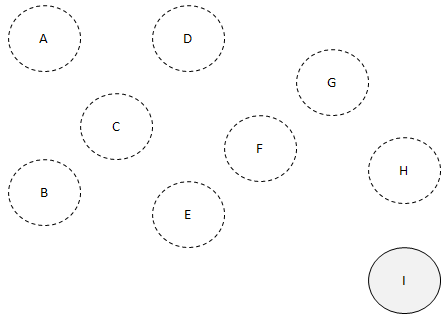

나머지 I도 얼른 제거합시다.

위상 정렬 결과입니다.

A B C D E F H G I

이 정도면 꽤 좋지요.

이해하기 쉽죠? 

일단 들어오는 간선의 수가 0인 노드를 방문해서 

그 노드의 진출 간선을 모두 제거하고 

또 다시 들어오는 간선의 수가 0인 노드를 잡고. 

만약 모든 노드를 방문하기 전에 끝났다면 

이 그래프는 DAG가 아니라는 소리죠. 

일단 이 처리는 해주시면 좋을 듯 하고요. 

자. 이번엔 다른 방법으로 해 보죠.

DFS, 즉 깊이 우선 탐색 방법으로 해보겠습니다.

DFS면 딱 생각나는 게 있죠?

갈 수 없는 길을 만날 때 까지 가 본다.

일단 두 노드가 있을 때는

알파벳 순으로 탐방을 하도록 합시다.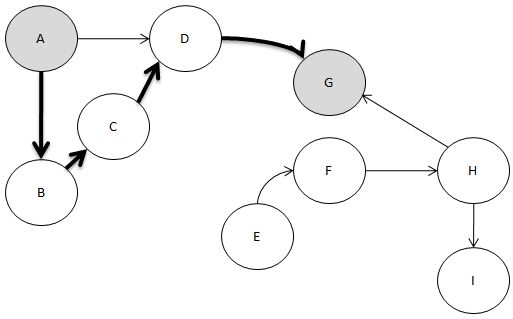

어휴. 자. 일단 진입 간선이

0인 노드를 찾는 데 걸리는 복잡도가 어느 정도 됩니까?

자. 들어오는 간선수를 저장해 뒀다면

단순히 O(V) 아니겠습니까?

이런 식으로 깊이 우선 탐색을 실시 합니다..

DFS 알고리즘은 제가 저번에 보여드린 듯 하고요.

여기서 하나 더 두어 볼까요?

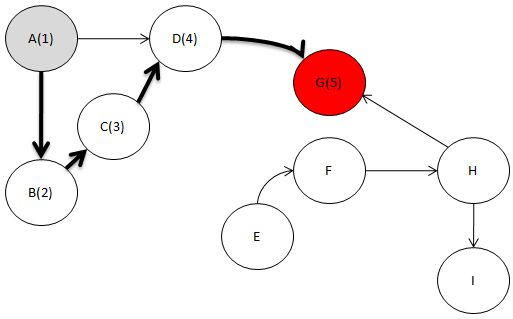
일단.. 갈 수 없을 때 까지 DFS를 합니다.

그리고 여기서 주목해야 할 것은..

다시 백 트래킹 하는 것입니다.

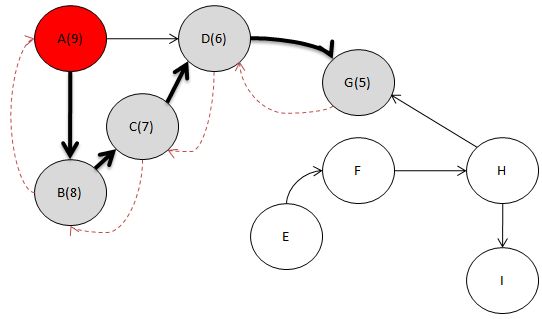
다시 오다니. 그게 무슨 소리요?

자. 일단 여기까지 수행했을 때

이렇게 삽입이 되어 있을 겁니다.

A B C D G

맞아요?

이 과정을 하나 하나 보여드리겠습니다.

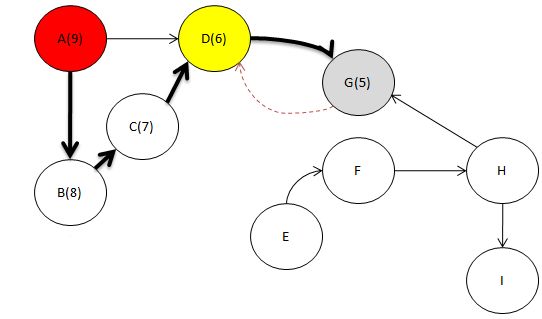
자. G로부터 거꾸로 올라가서

현재 D라는 녀석에 있다고 칩시다.

자. D와 인접하면서

깊이 우선 탐색으로 방문하지 않은 노드 있나요?

아니요. 없습니다.

따라서 D를 Head에 삽입을 해야 겠지요.

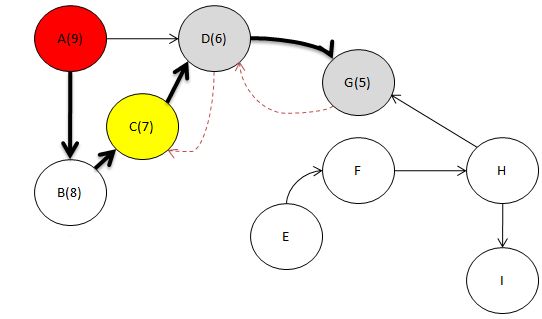
자. 이제 C를 봅시다.

역시 마찬가지입니다.

C와 인접하면서 DFS 탐색으로 방문하지 않은 노드 없죠?

따라서 C를 Head에 추가합니다.

이런 식으로 내가 먼저 깊이 우선 탐색을 한 것을

거꾸로 백 트래킹을 해 가면서

깊이 우선 탐색으로 방문하지 않았으면서

인접한 정점이 있다면

추가 작업을 해 줘야 겠지요.

자. 이제 또 다시 In 간선 수가 0인 노드를 찾죠.

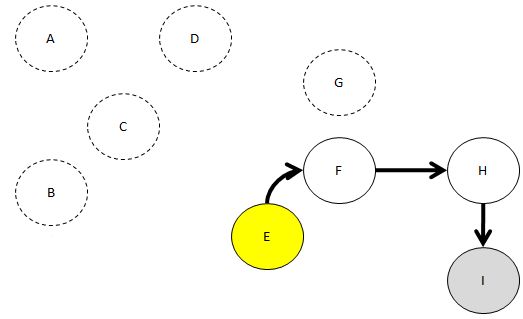
E로 들어오는 간선의 수가 0이군요.

자. 일단 DFS를 수행하면 다음과 같을 겁니다.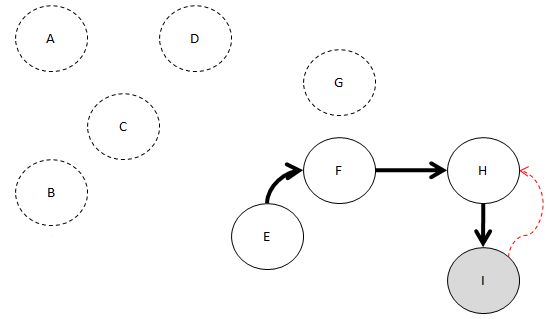

더 이상 갈 수 없는 길이 있네요.

I라는 녀석이 있죠?

여기서 부터 다시 백 트래킹 시작.

왔던 길을 다시 되돌아 가는 겁니다.

I 보세요. 더 이상 갈 수 없죠?

Head에 추가합니다.

일단 님들이 실행 시간을 숫자로 기록 해보시길.

규칙 찾으실 수 있습니다.

노드 H로 갑니다.

이미 I는 방문했는데..

H와 인접한 녀석 중에서 방문 안 한 녀석 없죠?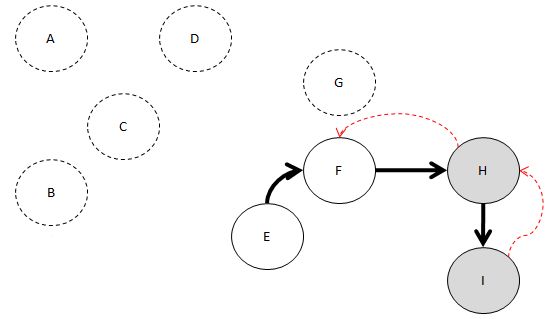

자. 이제 H를 Head에 넣고

다시 뒤로 갑시다.

F가 있군요. 그렇죠?

그런데 F 말이죠.

F와 인접하면서 방문하지 않은 노드 없죠?

그냥 F도 닥치고 Head에 추가합니다.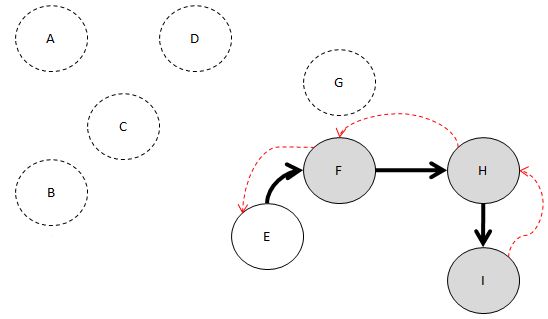

이제 E가 남았군요.

역시 마찬가지입니다.

E와 인접하면서 방문하지 않은 노드 없죠?

따라서 Head에 추가합니다.

만약에 이런 그래프였다면 어떨까요?

만약에 H의 인접 노드가 I가 아니라

I의 인접 노드가 H였다면 어떻게 되었을까요?

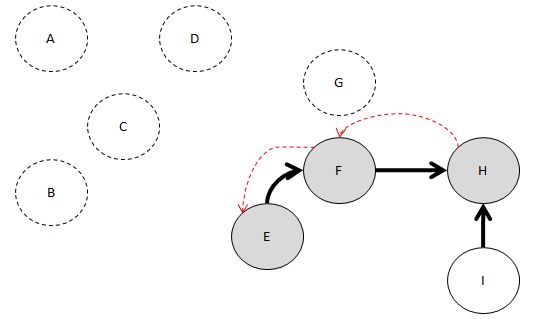
일단 이런 식으로 돌아오긴 할 겁니다.

그 다음에. I의 indegree 간선 수가 0이죠?

따라서 I를 Head에 추가하고 끝낼 겁니다.

사실 BFS로도 풀 거 같은데..

일단 DFS로 푸는 과정까지 보여드렸고요.

자. 이 것을 어떻게 링크드 리스트로 구현을 안 하고

배열로 구현을 해야 할 지 잘 생각해 보세요.

힌트는 실행 시간에 있습니다.

그것을 유심히 보시고요.

문제 하나 드리겠습니다.

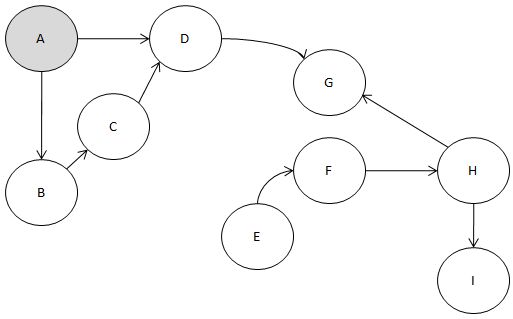
ⓓ : 문제

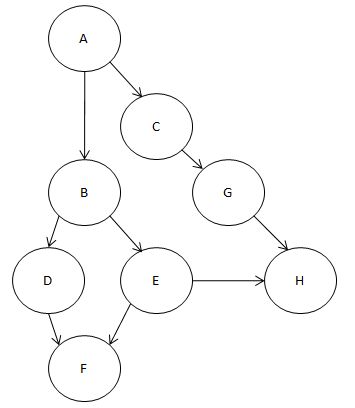
이 그래프를 DFS 방법으로 위상정렬 해 보세요.

물론 깊이 우선 탐색을 할 때

현재 내 위치로 부터 자식 노드가 2개 이상 있다면

알파벳 순으로 우선인 것을 먼저 잡으세요.

실행 과정을 그림으로 그리세요.

# :

덧글과 공감은

블로거에게 큰 힘이 됩니다

부모 노드를 기준으로, 왼쪽 자식은 부모보다 작은값, 오른쪽 자식은 부모보다 큰값을 갖는다

배열에서의 바이너리서치와 마찬가지로 한번씩 비교하면서 탐색 범위를 반씩 줄일 수 있다

배열과 비교해서, 동적으로 데이터의 삽입, 삭제가 이뤄질 수 있다

크게 탐색, 삽입, 삭제 기능이 있는데 삭제가 좀 까다롭다               

1. 자식노드가 없는 경우

2. 자식노드가 한개만 있는 경우

3. 자식노드가 두개 있는 경우

1번의 경우, 그냥 삭제하면 된다

2번의 경우, 삭제하려는 노드의 부모와 자식노드를 이어 주기만 하면된다

3번의 경우, 일단 삭제하려는 노드의 오른쪽 하위트리에서 최소값을 갖는 노드를 찾는다

(계속 왼쪽으로 내려갔을때 끝에 있는 노드가 최소노드 이다.)

그 최소노드를 삭제하려는 노드와 바꾼다

(그 최소노드가 삭제하려는거보다 큰 것들 중에서 제일 작으니까 왼쪽하위트리보단 크고, 오른쪽 하위트리보단 작게된다 올ㅋ)

나머지는 아래 소스를 보면 되겠다

각 함수들은 자신의 하위트리에 대해서 자신을 다시 recursive로 호출하는 형태이다
아 한가지 아쉬운점은, 트리가 한쪽으로만 엄청나게 쏠리게 되면 이진탐색이고 뭐고
그냥 리스트랑 다를게 없다. 검색효율이 걍 떨어지게 된다. 그래서 레드블랙트리란게 또 있다
#include "BinarySearchTree.h" BSTNode* BST_CreateNode(ElementType NewData){ BSTNode* NewNode = (BSTNode*)malloc(sizeof(BSTNode)); NewNode->Left = NULL; NewNode->Right = NULL; NewNode->Data = NewData; return NewNode; } void BST_DestroyNode(BSTNode* Node){ free(Node); } void BST_DestroyTree(BSTNode* Tree){ if( Tree->Right != NULL ) //오른쪽 자식있으면 똑같이 제거함수 호출해줌 BST_DestroyTree(Tree->Right); if( Tree->Left != NULL ) //왼쪽자식도 마찬가지 BST_DestroyTree(Tree->Left); Tree->Left = NULL; //다 없앴으면 NULL로 설정해줌 Tree->Right = NULL; BST_DestroyNode(Tree); //마지막에 루트노드를 없애줌 } BSTNode* BST_SearchNode(BSTNode* Tree, ElementType Target){ if( Tree == NULL ) //끝까지 갔는데도없으면 NULL return NULL; if( Tree->Data == Target ) //찾는 데이터와 일치하는 값을 갖는 노드를 리턴 return Tree; else if( Tree->Data > Target ) //찾는값이 현재노드보다 작으면 왼쪽으로 return BST_SearchNode(Tree->Left, Target); else return BST_SearchNode(Tree->Right, Target); } BSTNode* BST_SearchMinNode(BSTNode* Tree){ if(Tree == NULL) return NULL; if( Tree->Left == NULL ) //더이상 왼쪽자식이 없으면 지가 최소값 return Tree; else return BST_SearchMinNode( Tree->Left ); //왼쪽새끼 계속 따라가면 최소값나옴 } void BST_InsertNode(BSTNode* Tree, BSTNode* Child){ if( Tree->Data < Child->Data ){ //현재 노드보다 값이 크면 오른쪽으로 if( Tree->Right == NULL ) //오른쪽자식 없으면 거기다 삽입 Tree->Right = Child; else BST_InsertNode( Tree->Right, Child ); //있으면 그 자식에 대해서 또 삽입함수 호출 } else if( Tree->Data > Child->Data ){ //현재 노드보다 값이 작으면 왼쪽으로 if( Tree->Left == NULL ) Tree->Left = Child; else BST_InsertNode( Tree->Left, Child ); } } BSTNode* BST_RemoveNode(BSTNode* Tree, BSTNode* Parent, ElementType Target){ BSTNode* Removed = NULL; if( Tree == NULL ) return NULL; if( Tree->Data > Target ) //현재보다 값이 작으면 Removed = BST_RemoveNode(Tree->Left, Tree, Target); else if( Tree->Data < Target ) //현재값보다 값이 크면 Removed = BST_RemoveNode(Tree->Right, Tree, Target); else{ //원하는 값을 찾은경우 Removed = Tree; //잎 노드이면 바로 삭제 if( Tree->Left == NULL && Tree->Right == NULL){ if( Parent->Left == Tree ) Parent->Left = NULL; else Parent->Right = NULL; } //자식이 양쪽 다 있는경우 else{ if( Tree->Left != NULL && Tree->Right != NULL ){ BSTNode* MinNode = BST_SearchMinNode(Tree->Right); //최소값 노드는 현재노드의 오른쪽 하위트리에서의 최소값노드 //최소값 노드를 먼저 찾은 후 그 노드의 데이터를 갖는 노드를 지운다 //지우면서 트리는 재구성되고, 지운노드(최소값노드)는 다시 MinNode에 저장된다 MinNode = BST_RemoveNode(Tree, NULL, MinNode->Data); Tree->Data = MinNode->Data; } //자식이 하나만 있는경우 else{ BSTNode* Temp = NULL; if( Tree->Left != NULL ) Temp = Tree->Left; else Temp = Tree->Right; if( Parent->Left == Tree ) Parent->Left = Temp; else Parent->Right = Temp; } } } return Removed; } void BST_InorderPrintTree( BSTNode* Node){ if( Node == NULL ) return; //왼쪽 하위트리 출력 BST_InorderPrintTree( Node->Left ); //루트노드 출력 printf("%d ", Node->Data); BST_InorderPrintTree( Node->Right); }

내가 찾고자 하는값을 중앙값과 비교한다. 중앙값보다 크면 탐색범위를 오른쪽 반토막,

중앙값보다 작으면 탐색범위를 왼쪽 반토막으로 줄여나가면서 계속 반복한다, left가 right보다 크면 끝

1번 하면 전체 데이터 범위의 1/2, 2번하면 1/4, 3번하면 1/8.... x번하면 (1/2)^x 이 된다

전체 데이터가 n개이고 x번 서치하면 n(1/2)^x가 되는데, 이게 1이 되면 그때 찾은거니까 x를 구하면

x = logN이라는 훌륭한 성능을 갖게된다( 원래는 log2N인데 O(log2N) 은 O(logN)과 같으니까)

그리고 스탠다드 라이브러리에도 있다 원형은 다음과 같다

void *bsearch(const void *key, const boid *base, size_t num, size_t width, int (__cdecl *compare)(const void *, const void*) ); stl의 알고리즘에 있는 바이너리서치는 값이 있는지 없는지 존재만 판별해주지만,

이건 친절하게 그 값의 주소를 알려준다(근데 왜 리턴이 보이드지 @.@???)

int Partition(int DataSet[], int Left, int Right){ int First = Left; int Pivot = DataSet[First]; //맨 처음요소를 기준으로 잡는다 ++Left; while(Left <= Right){ while( DataSet[Left] <= Pivot && Left <= Right) ++Left; //왼쪽에서부터 출발해서 기준보다 큰 요소를 찾는다 while( DataSet[Right] >= Pivot && Left <= Right) --Right; //오른쪽부터 출발해서 기준보다 작은 요소를 찾는다 if( Left < Right) Swap(DataSet[Left], DataSet[Right]); //위에서 찾은 큰거와 작은거를 바꿔줌 else break; } Swap(DataSet[First], DataSet[Right]); //기준과 왼쪽집합의 끝요소를 바꿔준다 return Right; } void QuickSort(int DataSet[], int Left, int Right){ if(Left < Right){ int Index = Partition(DataSet, Left, Right); //기존의 집합을 쪼갠후 쪼개진 인덱스를 반환 QuickSort(DataSet, Left, Index-1); QuickSort(DataSet, Index+1, Right); } } 성능분석을 해보자

맨처음의 n개로 이루어진 집합을 하나하나씩 다 쪼개야하는데

2개로 쪼개는데 1번, 4개로 쪼개는데 2번, 8개로 쪼개는데 3번....

아 그럼 n개로 쪼개는데는 lon(2)n 번만큼의 호출이 필요하다

그리고 Partiton()에서는 앞에서, 뒤에서 각각 비교를 하는데 n번 비교한다 n개의 원소가 있으니까

2개로 쪼개지면 n/2 + n/2 = n, 4개로 쪼개지면 n/4 + n/4 + n/4 + n/4 = n 으로 결국 모두 n번 비교한다

그래서 총 회수는 nlog(2)n 이다<p>

디바이드 앤 퀀커의 한 종류란다<p>

void qsort(void *base, size_t num, size_t width, int(_cdecl *compare)(const void *, const void *)); 순서대로 데이터 집합의 배열주소, 데이터요소의 개수, 한 데이터의 크기, 비교함수에 대한 포인터이다

나머지는 다 알겠는데 맨 마지막에 인자가 뭔가 요상하다

다음과 같이 매번 작성해줘야 한다

int Compare(const void *_elem1, const void *_elem2){ int *elem1 = (int*)_elem1; int *elem2 = (int*)_elem2; if( *elem1 > *elem2 ) return 1; else if( *elem1 < *elem2 ) return -1; else return 0; } 데이터의 자료형에 따라 첫째, 둘째 줄을 수정해주어야한다

하는 역할은 stl의 compare함수와 비슷한 것 같다

다이나믹이니 dfs니 뭐니 그런거 한다고 깝치다가 더 기본적인걸 무시하고 있었군

기본중의 기본인 버블정렬, 삽입정렬도 제대로 구현못하다니 짱난다

일단 버블소트

for(int i=0; i<10; i++) for(int j=0; j<10-i; j++) //매번 첫번째 원소부터 시작해서 비교하는데 //한번 돌고나면 배열의 끝에는 가장 큰수가 있으므로 비교횟수가 1번씩 줄어든다 if(a[j] > a[j+1]) //앞에놈이 뒤에꺼보다 크면 바꿔 swap(a[j], a[j+1]); 그리고 삽입정렬

for(int i=1; i<10; i++){ //비교하는 배열이 두개, 세개... 늘어남 if( a[i] < a[i-1] ){ //그전거는 다 정렬되어있으니 앞에놈이랑만 비교해보면돼 int j=i; while( a[i] <= a[j] ) //자기보다 작은놈 나올때까지 인덱스 줄임 j--; j++; //내가 원하는 인덱스보다 하나 더 줄었으니 증가해주고 int tmp = a[i]; memmove(&a[j+1], &a[j], sizeof(a[0])*(i-j)); //쭉 땡겨주고 a[j] = tmp; //빈자리에 삽입 } } 저기있는 memmove는 string.h에 포함되어있고, 이름그대로 메모리를 이동시킨다

첫번째 인자는 새로 옮길주소, 두번째는 원본데이터의 주소, 세번째는 이동시킬 데이터의 양이다

a[0]가 4byte니까 4*(i-j) 바이트만큼 옮겨준다

memmove는 처음본다 쩝

버블이나 삽입이나 둘다 시간복잡도는 O(n^2)이라서 둘다 병신인데

버블은 정렬된 상태에서도 비교를 하나하나 다하지만

삽입은 정렬된 상태이면 비교를 안하니까 좋단다

꿈틀꿈틀 알고리즘,

이론은 쉽지만 구현할때 반복하는 조건이나 값의 인덱스가 헷갈린다 많이많이

연습 많이 해봐야할듯

#include #include using namespace std; int N, a[4000005]; bool era[4000005]; int main(void){ // freopen("input.txt", "r", stdin); scanf("%d", &N); fill(era+2, era+N+2, true); for(int i=2; i*i<=N; i++) if( era[i] == true ) for(int j=i+i; j<=N; j+=i) era[j] = false; int idx=0; for(int i=1; i<=N; i++) if( era[i] == true ) a[idx++] = i; int s=0, t=0, count=0, sum=0; while( !(s==idx && t==idx)){ //머리와 꼬리 모두 끝까지 갈때까지 if(sum == N){ //원하는 합이 나오면 꼬리부분을 빼줌 count++; sum -= a[s++]; } else if(sum < N && t< idx) //찾는 합보다 작으면 머리 더해주고 sum += a[t++]; else if(sum > N && s< idx) //찾는 합보다 크면 꼬리를 빼줌 sum -= a[s++]; else break; } printf("%d\n", count); return 0; }

dp를 이용해서 푸는 문제, 일단 iterative로 풀면

d[1][1] = A[1][1]; for(int i=2; i<=N; i++) for(int j=1; j<=i; j++) d[i][j] = max( d[i-1][j-1], d[i-1][j]) + A[i][j]; 대충 이렇게 할수 있는데 이걸 recursive로 하면

int cache[505][505]; //(y, x)위치부터 맨 아래줄까지 내려가면서 얻을 수 있는 최대 경로의 합을 반환 int path(int y, int x){ //기저 사례 if(y == N-1) return a[y][x]; //메모이제이션 int& ret = cache[y][x]; if(ret != -1) return ret; return ret = max(path(y+1, x), path(y+1, x+1)) + a[y][x]; } 이렇게 recursive함수를 만들 수 있다 recursive는 처음이라 문화컬쳐

큰 차이는 iterative는 위에서 아래로 내려가지만 

recursive는 아래에서 위로 올라가도록 구성했다는 것이다

어떤게 더 빠른지는 잘 모르겠는데 boj랑 알고스팟에서 실행시간이 달랐다 테스트케이스가 달라서 그런듯

듣자하니 메모이제이션을 사용하다가 호출을 존나게 하다보면 스택 오버플로우가 발생할수도 있다고 한다

또 듣자하니 잘하는사람은 dp를 할떄 recursive로 한단다 난 벌레니까 iterative로 해야지

근데 고수될려면 recursive로도 해봐야겠다

참고로 모든 iterative로 만든 프로그램은 recursive형태로 바꿀수 있고 그 반대도 가능하다고 한다

기본적인 방법은 dp로 해결 할 수 있겠다

#include #include using namespace std; int N; int A[1005]; int d[1005]; int main(void){ // freopen("input.txt", "r", stdin); scanf("%d", &N); for(int i=0; i<N; i++) scanf("%d", &A[i]); for(int i=0; i<N; i++) d[i] = 1; for(int i=0; i<N; i++) for(int j=0; j<i; j++) if( A[j] < A[i] ) d[i] = max(d[i], d[j]+1); int ans = 0; for(int i=0; i<N; i++) ans = max(ans, d[i]); printf("%d\n", ans); return 0; } 약간 쉬운 다이나믹이긴한데 O(n^2)이라 n이 커지면 시간이 오래 걸릴거 같다 그래서 두번째로 더 좋은 방법은 lower_bound를 쓰는 것이다 #include #include #include using namespace std; int N; int a[1005]; int LIS[1005]; int main(void){ // freopen("input.txt", "r", stdin); scanf("%d", &N); for(int i=0; i<N; i++) scanf("%d", &a[i]); fill(LIS, LIS+N, 999999999); for(int i=0; i<N; i++) *lower_bound(LIS, LIS+N, a[i]) = a[i]; printf("%d\n", (int)(lower_bound(LIS, LIS+N, 999999999)-LIS)); return 0; } 코드도 더 간결하고 lower_bound는 binary search를 사용하기 때문에

이 코드의 시간복잡도는 O(nlogn)이 된다

채점할때도 시간차가 좀 느껴지는것 같다

근데 중요한것 이 방법을 이용하면 LIS의 길이만 알뿐, 실제 들어가 있는 값은 상관없다는것이다

바이너리 서치하다가 위그림 같은 상황이 되었다고 하자

내가 지금 찾으려는 값보다 작으면 현재의 mid는 답이 아니라는 소리고

 left가 mid로 바뀌게 될 것이다

그리고 새로운 미드를 (left+right)/2;로 한다면

새로운 mid는 이전의 mid와 같은 값을 갖게되고, 그 이후로도 계속 left와 mid는 

같은값을 갖게되어 무한루프에 빠지게 된다

그래서 이런경우에는 left를 mid로 바꿔준후

이래 해주면 새로운 mid는 이전의 mid가 아닌 right로 새로운 값을 갖게 된다

그리고 그 mid가 내가 찾는 답이 될것이다