푸리에 변환
푸리에 변환(Fourier transform)은 한 함수를 인자로 받아 다른 함수로 변환하는 선형 변환이다. 일반적으로 변환된 함수는 원래 함수를 주파수 영역으로 표현한 것이라고 부른다.
함수 x(t)가 복소수 범위에서 정의되어 있고 르베그 적분이 가능할 때, 이 함수의 푸리에 변환 X(ξ)는 다음과 같이 정의된다.
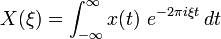(ξ는 모든 실수 범위)
여기서 일반적으로 독립변수 t는 시간을 나타내고, 변환변수 ξ는 주파수를 나타낸다.
X(ξ) 대신 
, 
와 같은 표기를 사용하기도 한다.
푸리에 역변환은 다음과 같다.
(t는 모든 실수 범위)- 푸리에 급수,변환에 대해 개념만 간단하게 말해드리면,신호를 어떻게 표현할수 있을까요?
- 사인파 같은 신호는 시간의 영역에서 쉽게 꼬부랑 그릴수 있습니다.
그럼 정현사인파를 시간의 영역이 아니 주파수의 영역에서 그리면 어떻게 됩니까
양 음의 주파수구간에서 작대기 하나씩 서있는 모양입니다.그럼 2개면,양음에서 작대기2개씩생기겠죠.이건 시간의 영역으로 넘기면(푸리에 역변환) 정현적인 사인파가아닌 두개의주파수성분이 합쳐진 꼬부랑꼬부랑파형이됩니다. - 구형파를 푸리에 트랜스폼하면 모든 주파수성분에서 크기를 가지는 Sa함수가되는것이죠.구형파는 각각의 무수한 정현파로 표현할수 있단겁니다.
무수한 정현파에서 크기는 푸리에 계수가 됩니다. - 잡음같은 신호도 푸리에변환하면 모든 주파수영역에서 일정한 크기를 가지는 신호로표현됩니다.
- 이게 뭐냐 푸리에 변환이란게 신호를 시간의 영역에서 주파수의 영역으로 변환해서표현하는 수학적도구로 전자공학에서는 사용하는것입니다. 또한 푸리에급수는 주기신호 푸리에 변환은 비주기신호에서 사용합니다.
- 푸리에변환은 푸리에 급수의 확장이라 생각하세요
- 왜쓰냐 ? 주파수영역에서 보면 신호를 시간의 영역에서 볼수 없던 부분이나 이점들이 있어서입니다.푸리에트랜스폼이 안쓰이는 전자공학분야는 거의 없다고 생각하시면 되니 열심히 하셔야겠죠..시간의 영역과 주파수영역에 대한 개념을 잘 잡아야됩니다.
