반갑습니다. 위대한 교주 LGS입니다. (모두들 교주를 찬양합시다)
System을 표현 하는 방법중에는 Transfer function을 담고 있는 Block(네모난 상자)들을 서로 연결하여
Graphical 하게 System을 표현하는 방법도 있습니다. 각 Block은 System을 이루는 각 부품을 표현하는 TF일꺼구요~
Block으로 이루어진 그림을 Block Diagram이라고 그래요.
오늘은 이 Transfer function Block을 가지고 놀아보죠~ ^^

만약 Block diagram에서 Transfer function이 series(직렬)로 연결되어 있으면 ... 둘을 곱하면 됩니다.
Control System Toolbox에서 series라는 함수를 제공하고 있지만 (G = series(G1,G2) ) 굳이 series라는 함수를 사용하실 필요 없이
그냥 간단하게 G = G1 * G2 라고 하시면 됩니다.

Transfer function이 parallel(병렬)로 연결되어 있으면 둘을 더하면 되구요
역시 Control System Toolbox에서 parallel이라는 함수를 제공하고 있지만(G = parallel(G1,G2) ) 그냥 G = G1 + G2 라고 하셔도 됩니다.
여기까지는 문제 없으시죠? ^^
자 다음 Feedback을 포함하고 있는 closed loop를 봅시다~

E(s)는 실제 output Y(s)와 내가 원하는 값 X(s) 사이의 차이(Error)를 말합니다.
그러므로 E(s) = X(s) - Y(s)가 될꺼구요 ( (-)가 붙은 것에 주의하세요~ )
Feedback 신호에 (-)마이너스가 붙은 녀석을 Negative Feedback이라고 합니다.
H(s)는 센서 같은 녀석의 transfer function이구요. (G(s)는 plant(실제 작동하는 녀석)의 TF겠죠?)
전체 Transfer function은 Y(s) = E(s)G(s) 와 E(s) = X(s) - E(s)G(s)H(s) 를 연립해서 푸시면 쉽게 구하실 수 있습니다. ^^
계산을 해보시면 feedback loop의 transfer function은 Geq(s) = G(s)/[1+H(s)G(s)] 가 되네요
(Negative Feedback인 경우 Geq가 G(s)/[1+H(s)G(s)] 라는 정도는 외워두시면 편합니다.)
MATLAB에서 closed loop의 전체 transfer function을 계산하시려면 feedback이라는 함수를 사용하시면 되요~ =(=^ㅅ^=)=
G_eq = feedback(G,H)라고 하시면 equivalent transfer function을 얻으 실 수 있습니다.
예를 들어 G(s) = 1/(s+2) , H(s) = 1/(s+3) 이라고 한다면 TF는?? 넵~ 잘하셨습니다 ㅎㅎ


아주 간단한 녀석으로 연습 하나 더 해보고 가겠습니다. ^^

간단하다고 한건 훼이크였구요 ;; (죄송) 조금만 복잡해져도 머리속이 복잡해집니다요 ㅜㅜ
위의 Block diagram을 다른 방법으로 표현해보겠습니다.

위와 같이 생긴 그림을 Signal-flow graph라고 해요.
Block diagram에서 Signal-flow graph로 변경하는 것 척!봐도 아시겠죠? ^^
Node(신호가 쪼개지거나 합쳐지는 지점)만 잘 잡으시고 부호만 신경 써주시면 땡입니다요~ o(^o^)o
위의 복잡한 Signal Flow Chart(또는 Block Diagram)를 팍 뭉뚱그려서 한개의 Block으로 만드는 방법이 있습니다.
이름하야 (Mason 아져씨가 만들었다 하여) Mason's Rule !! 두둥!!
Mason's Rule을 적용하시려면 우선 3가지를 구해 주셔야 합니다.
Forward-path gain, Loop gain, 그리고 마지막으로 Nontouching-loop gain !!
Forward-path gain 부터 보죠~
Forward-path gain은 말 그대로 input X(s)에서 output Y(s)로 가는 모든 길을 말합니다. 단 중간에 뒤로 돌아올 수 없습니다.
무조건 앞으로만 전진하여 X(s)에서 Y(s)로 가는 모든 길을 찾아주시면 됩니다.


위의 예제의 경우 Forward-path가 2개가 있네요~ 그러므로

이 됩니다.
두번째로 Loop gain. 말그대로 빙글빙글 도는 Loop를 모두 찾아주세요. 화살표 방향 잘보시고요~

아 복잡하군요 ^^;; 각 Loop를 따로 그려보면

Loop gain을 정리해봅시다요. o(^o^)o

마지막으로 Loop들끼리 Nontouching-loop gain을 찾아주시면 끝~
1번 loop와 2번 loop는 서로 노터치 하고 있네요. 그리고 1번 loop와 3번 loop도 노터치이구요~
2번,3번은 서로 터치합니다. 그러니까 Nontouching-loop gain에서 제외!!
(지금의 예제에서는 없지만 만약 3개,4개, 등등...의 Loop가 서로 독립적이라면 모든 조합을 다 적어주세요~)

자~ 이제 위에서 구한 Forward-path gain, Loop gain, Nontouching-loop gain을 Mason 아져씨가 잘 정리해둔 Mason's Rule에
대입하면 끝~ =(=^ㅅ^=)=

여기에서 Δ는 1 - (모든 Loop gain의 합) + (모든 2 Nontouching-loop gain의 합) - (모든 3 Nontouching-loop gain의 합) - (모든 4 .....) 입니다.
지금의 예에서는 2 Nontouching-loop gain 밖에 없네요 ^^
Pk는 K번째 Forward-path gain이구요~ Δk는 K번째 Forward-path gain와 노터치하는 Loop의 Δ를 계산해주시면 됩니다.
지금은 모든 Loop가 Forward path랑 다 접하고 있어 Δk는 모두 1입니다.
Mason's Rule을 하시다보면 아~ 귀찮아요 -_-;; 흑묘든 백묘든 쥐만 잘 잡으면 됩니디요~ 깜장 고양이든 흰둥이 고양이든... 냠
훨씬 간단한 방법이 있습니다. 대단히 대단하고 엄청히 엄청난 여러분의 교주가
Simulink로 Block diagram을 그리고 Simulink model에서 바로 Transfer function을 뽑아내 보겠습니다. ^^ (Simulink의 간단한 사용법)
우선 Simulink로 보이는 대로 들리는 대로 상상하는 대로 사이버 Simulink Model 하나 만드시구요~ (기타로 오토바이 타자!!)

위의 System은 G(s) = 1/s고 H(s)는 1이니까 Geq(s) = 1/(s+1)로 암산으로도 계산 할 수 있으시죠? =(=^ㅅ^=)=
우선 Constant와 node(동그라미 안에 +-있는 녀석) 사이의 선을 선택하신 후 마우스 오른쪽을 클릭 -> Linearization Points -> Input point를 클릭하여
Input point를 만듭니다.

다음으로 Integrator(1/s)와 Scope 사이의 선을 선택하신 후 위와 같은 방법으로 Output point를 만들어 주세요~
그러면 Input point와 Output point를 확인 할 수 있는 표시가 생깁니다.

다음으로 Menu의 Tools -> Control Design -> Linear Analysis ... 를 클릭하셔서...

Linear Analysis Tool을 띄워주세요.

EXACT LINEARIZATION Tab에서 녹색 삼각형 Linearize 아이콘을 폭풍 클릭!!

그러면 Linear Analysis Workspace에 linsys1 State Space(ss) class 변수가 생성된 것을 볼 수 있습니다.
(Plot Result에서 Step, Impluse 등 그래프도 바로 그릴 수 있습니다.)
사실 위에서 했던 것은 Nonlinear Simulnik 모델을 Linearization하는 과정이었구요~ 우리는 linsys1을 얻기 위해 위의 과정을 수행하였습니다.
자~ 마지막으로 Linear Analysis Workspace에 있는 linsys1을 MATLAB Workspace로 Drag & Drop 하시면 짠!!
MATLAB Workspace에 linsys1 ss model이 복사됩니다.

State Space(SS) model을 Transfer Function(TF) model로 변환하시려면 그냥 tf 함수를 사용하시면 됩니다.
(model간 변환은 추후에 다루도록 하겠습니다.)

Very Good!! 맞게 나오네요 o(^o^)o
위대한 교주의 능력!! ㅋㅋ
자~ 이번시간은 여기서 마무리하죵~
다음시간에 뵙겠습니다. 이만...
첨부 (30)
'DSP' 카테고리의 다른 글
| convolution - C++ 구현 (0) | 2015.04.03 |
|---|---|
| rect func fourier transform (0) | 2015.03.26 |
| causal vs noncausal (0) | 2015.03.23 |
| fourier property (0) | 2015.03.16 |
| Properties of Fourier Transform (0) | 2015.03.16 |





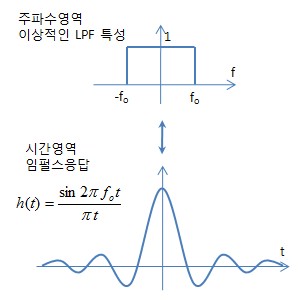 - 따라서, 이상적인
- 따라서, 이상적인 





![$\displaystyle \int_{-\infty}^\infty x(t)y^*(t) dt
=\int_{-\infty}^\infty x(t) [\frac{1}{2\pi}\int_{-\infty}^\infty Y^*(j\omega)e^{-j\omega t}d\omega]dt$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img145.png)
![$\displaystyle \frac{1}{2\pi}\int_{-\infty}^\infty Y^*(j\omega)[\int_{-\infty}^\...
...dt] d\omega
=\frac{1}{2\pi}\int_{-\infty}^\infty X(j\omega)Y^*(j\omega) d\omega$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img146.png)

![$\displaystyle \frac{1}{2\pi}\int_{-\infty}^\infty \vert X(j\omega)\vert^2e^{j\o...
...infty}^\infty S_X(j\omega) e^{j\omega\tau}d\omega
= {\cal F}^{-1}[S_X(j\omega)]$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img159.png)
![$\displaystyle \int_{-\infty}^\infty [ \int_{-\infty}^\infty
x(\tau)y(t-\tau)d\tau] e^{-j\omega t} dt$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img164.png)
![$\displaystyle \int_{-\infty}^\infty x(\tau) [ \int_{-\infty}^\infty
y(t-\tau) e^{-j\omega t} dt] d\tau$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img165.png)
![$\displaystyle \int_{-\infty}^\infty x(\tau) e^{-j\omega \tau}[ \int_{-\infty}^\infty
y(t-\tau) e^{-j\omega(t-\tau)} d(t-\tau)] d\tau$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img166.png)

![$\displaystyle \int_{-\infty}^\infty [\frac{1}{2\pi}\int_{-\infty}^\infty
X(j\omega') e^{j\omega't} d\omega'] \; y(t) e^{-j\omega t} dt$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img170.png)
![$\displaystyle \frac{1}{2\pi}\int_{-\infty}^\infty X(j\omega') [ \int_{-\infty}^\infty
y(t) e^{j\omega't} e^{-j\omega t} dt] d\omega'$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img171.png)
![$\displaystyle \frac{1}{2\pi}\int_{-\infty}^\infty X(j\omega') [\int_{-\infty}^\infty
y(t) e^{-j(\omega-\omega')t} dt] d\omega'$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img172.png)



![$\displaystyle \frac{1}{2\pi}\int_{-\infty}^\infty [j\omega X(j\omega)] e^{j\omega t} d\omega
= {\cal F}^{-1} [j\omega X(j\omega)]$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img177.png)

![\begin{displaymath}X(j\omega)={\cal F}[x(t)]=\frac{1}{j\omega}{\cal F}[ \frac{d}{dt}x(t) ] \end{displaymath}](http://fourier.eng.hmc.edu/e101/lectures/handout3/img181.png)
![\begin{displaymath}{\cal F}[u(t)]=\frac{1}{j\omega}{\cal F}[ \frac{d}{dt}x(t)]=
\frac{1}{j\omega}{\cal F}[ \delta(t)]=\frac{1}{j\omega} \end{displaymath}](http://fourier.eng.hmc.edu/e101/lectures/handout3/img182.png)
![\begin{displaymath}{\cal F}[sgn(t)]=\frac{1}{j\omega}{\cal F}[ \frac{d}{dt}sgn(t)]=
\frac{1}{j\omega}{\cal F}[ \delta(t)]=\frac{1}{j\omega} \end{displaymath}](http://fourier.eng.hmc.edu/e101/lectures/handout3/img183.png)

![$\displaystyle \frac{d}{d\omega}[\int_{-\infty}^\infty
x(t)e^{-j\omega t}dt]
=\int_{-\infty}^\infty x(t)\frac{d}{d\omega}e^{-j\omega t}dt$](http://fourier.eng.hmc.edu/e101/lectures/handout3/img200.png)






